WAS BACH A MATH3MAT1C1AN?
© by John Bertalot from lectures he gave in
King’s College, Cambridge, August 1986
Southwell Minster, July 2000
The Hereford Three Choirs’ Festival, August 2003
and Blackburn, September 2010
6. If Bach did it twice, he must have meant it!
We saw, at the end of my 5th article, that Bach wrote his name in music at significant places in at least two of his compositions (Bb in Germany is 'B' and B natural is 'H'):
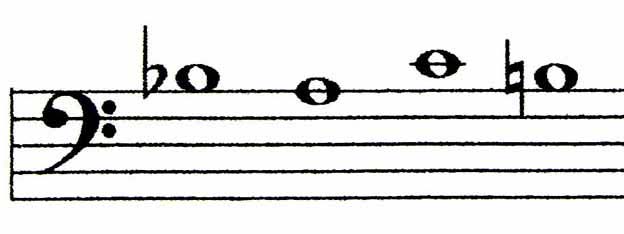
(i) at the exact centre of the Schübler Chorale Preludes - the Preludes which define the walk of a Christian, and (ii) towards the end of the last fugue in the Art of Fugue which, alas, is unfinished, because he died ... but not before placing his musical signature in notes (Bb - A - C - B natural) in this collection of fugues in which he displayed all his amazing contrapuntal skills.
Therefore taking this hypothesis let's look at some more pairs of 'did he mean it'.
An obvious example is his set of 48 Preludes and Fugues.
He wrote the first 24 to demonstrate that the tuning of a keyboard should be such that music could be played in any key.
Did he mean it? Yes, by composing a second set.
But there's more:
Look at the 24th Fugue subject in B minor in the first set: you'll see that he has all twelve semitones. (This was 150 years before Schoenberg's 12-note music!) ... although, of course Bach used more than 12 notes to be able to achieve this ultimate chromaticism.

Did he mean to use all twelve notes of the chromatic scale - or was it an accident? If he meant it, then he would have a quasi-12-note 'subject' somewhere in the second set of the 48.
And he did: look at the beginning of the 20th Prelude of the second set where he manages to get all twelve chromatic notes within the very first bar:

We mentioned how important the number 14 was to Bach. (For in alphabetical numerology B+A+C+H = 14)
In 1733 he designed his own logo.
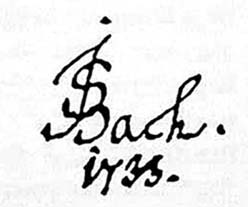
Count the number of letters, the number of figures and the number of dots.
I can't remember where I found this, but the writer said that he couldn't think why Bach chose the year 1733 to do this.
Of course, you know why!
He later designed another logo which is now used extensively for Bach's music, although not everyone understands why.
Here it is as Bach designed it. What can you see?

With colour added, it's clear what JSB did - for, as we've noted elsewhere, he was a composer who could write music not only going forwards but also backwards (retrograde).


The new organ in St. Thomas' Church, Leipzig, has this logo on its front case:

And to finish this section,
a mind-blowing example of Bach's mathematical skills.
Look at the Orgelbüchlein again - the two Chorale Prelude on Aus tiefer Noth... (Out of the deep have I called unto Thee, O Lord - Psalm 130)
Even though these Preludes are based on the same chorale melody, they are of different lengths.. Each has its first section repeated.
The Prelude for manuals only has 72 bars if the repeated bars are not counted, but 100 if they are.

The Prelude with (double) pedals has 54 bars if the repeated bars are not counted, but 75 if they are.

Now this is where Bach's extraordinary mathematical skills can be revealed, for the proportions of each Chorale Prelude are identical, when one divides the full number of bars by the the number of bars without repeats:
100 divided by 72 = 1.388888(recurring)
75 divided by 54 = 1.388888(recurring)
And, of course, 1.388888(recurring) to one decimal point is 1.4
Well, you may think, that must be a coincidence – unless, of course, he's done it again.
Yes, he has, in his Mass in B minor.
See a following article!
And one can discover yet another amazing mathematical proportion in these two Chorale Preludes:
The number of complete bars in one Prelude can be divided into the other.
The number of incomplete bars in one Prelude can be divided into the other.
100 divided by 75 = 1.33333 (recurring)
72 divided by 54 = 1.33333 (recurring)
In other words, the lengths of the two Chorale Preludes, with and without repeats, are proportionally identical.
But there is one more mathematical delight to be gotten from these two Chorale Preludes which are based on the 130th Psalm.
The total number of bars actually written (ignoring repeats but counting 1st & 2nd time bars)
is 75 in the Manual version
and
55 in the Double Pedal version.
75+55 = 130
75 divided by 55 = 1.383838 (recurring)
or 1.4 to one decimal point.
!